Ludolfovo číslo

Výpočet Pí na 201 desetinných míst

Venca Bartáček, spolužák z MFF UK a kamarád, udělal v roce 1994 program v Pascalu na výpočet Ludolfova čísla π (Pí) na 201 desetinných míst 
3.1415926535 8979323846 2643383279 5028841971 6939937510
  5820974944 5923078164 0628620899 8628034825 3421170679
  8214808651 3282306647 0938446095 5058223172 5359408128
  4811174502 8410270193 8521105559 6446229489 5493038196
  4

Čas výpočtu: 3 minuty 59 sec
Program: zatím v Pascalu, později bude v Céčku
Počítač: 80386SX - 33MHz
Kde: V Písku 8.1.1994
Kdo: Václav Bartáček (toho času student MFF UK v Praze)

Od té doby uplynulo hodně času…

A dnes?

Algoritmus pro výpočet Ludolfova čísla Pí

Výpočet π metodou Monte Carlo

Máme-li čtverec a do něj vepsanou kružnici, výběrem nekonečného počtu pseudonáhodných bodů uvnitř čtverce získáme čtvrtinu Ludolfova čísla π (Pí), jako podíl počtu zásahů dovnitř kružnice a vně kružnice. Výpočet pomocí metody Monte Carlo je zatížen chybou generátoru psaudonáhodných čísel a pro daný počet pokusů těžko určíme přesnost, s jakou se výsledek číslu π (Pí) blíží.

Podíl obsahů čtverce a do něj vepsané kružnice je čtvrtina čísla Pí

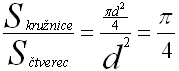
Podíl obsahů čtverce a do něj vepsané kružnice je čtvrtina čísla Pí - Výpočet π metodou Monte Carlo

Výpočet π jako součet nekonečné matematické řady

Nekonečná matematická řada je nejoblíbenější způsob vyčíslení π (Pí). Při výpočtu snadno vysledujeme velikosti přírůstků v každém kroku, takže jsme schopni určit přesnost výsledku v závislosti na počtu kroků výpočtu.

Příklady matematických řad pro výpočet Pí

Rychlost výpočtu (mimo optimalizace algoritmu) záleží na výběru matematické řady, protože rychlost konvergence jednotlivých řad k číslu π (Pí) se výrazně liší.

Pi = 4*( 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... )

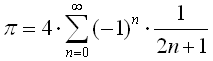
Pi = 4*( 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... ) - Matematické řady pro výpočet Pí

Pi = 4*( (1/2+1/3) - (1/2^3+1/3^3)/3 + (1/2^5+1/3^5)/5 - (1/2^7+1/3^7)/7 + ... )

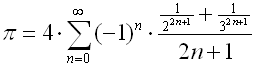
Pi = 4*( (1/2+1/3) - (1/2^3+1/3^3)/3 + (1/2^5+1/3^5)/5 - (1/2^7+1/3^7)/7 + ... ) - Matematické řady pro výpočet Pí

Pi = 4*( (4/5-1/239) - (4/5^3-1/239^3)/3 + (4/5^5-1/239^5)/5 - (4/5^7-1/239^7)/7 + ... )

Pi = 4*( (4/5-1/239) - (4/5^3-1/239^3)/3 + (4/5^5-1/239^5)/5 - (4/5^7-1/239^7)/7 + ... ) - Matematické řady pro výpočet Pí

Příklady výsledků výpočtu Pí

Pro srovnání s Vencou uvádím (užitím 2. a 3. matematické řady výše) současné výsledky ze dne 15.5.2012, počítané pomocí BCMath v linuxovém PHP 5.2.10 (cli) procesorem Intel(R) Core(TM)2 Duo E4500 na 2.20GHz. Abych zabránil chybě posledních číslic, celý výpočet probíhal s přesností o 2 desetinná místa vyšší než je výsledek zobrazen. 1.matematická řada výše konverguje proti uvedeným dvěma extrémně pomalu, proto chybí, pro výpočet Ludolfova čísla π (Pí) je neefektivní.

Výpočet π na 201 desetinných míst dle 2.řady

Program pro vypocet Pi = 4*( (1/2+1/3) - (1/2^3+1/3^3)/3 + (1/2^5+1/3^5)/5 - (1/2^7+1/3^7)/7 + ... )

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964

Desetinnych mist: 201
Vypocetnich cyklu: 333
Delka vypoctu: 0.011015892028809s

Výpočet π na 201 desetinných míst dle 3.řady

Program pro vypocet Pi = 4*( (4/5-1/239) - (4/5^3-1/239^3)/3 + (4/5^5-1/239^5)/5 - (4/5^7-1/239^7)/7 + ... )

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964

Desetinnych mist: 201
Vypocetnich cyklu: 145
Delka vypoctu 0.0047039985656738s

Zdrojové kódy výpočtů Pí na 201 desetinných míst

Pro všechny zájemce o matematiku nebo z řad vývojářů software jsem zdrojové kódy k výpočtu Ludolfova čísla π (Pí) dle uvedených matematických řad v jazyce PHP převedl na GitHub do Calculating Pi (pouze anglicky).

Další stránky pro volný čas

Rubikova kostka - Návod na složení 13.6.2004 - popis a návod na složení Rubikovy kostky
Úvod do Matfyzáka - Legendární povídka z prostředí MFF UK - dílo neznámého autora přibližně z roku 1992, které pro svoji nadčasovost stále stojí za to

Malá násobilka do 25 - Kvíz na procvičování násobení pro výuku matematiky 2. třídy 🔢㉕
Malá násobilka do 100 - Kvíz na procvičování násobení pro výuku matematiky 2. třídy 🔢⏳
Velká násobilka - Kvíz na procvičování násobení pro výuku matematiky 3. třídy 🔢⌛

Možnost podpory mé tvorby

Tato moje soukromá webová tvorba je k dispozici zcela zdarma. Pokud mě ale chcete finančně podpořit, přijmu to rád (momentálně jsem bez příjmů) a předem velice děkuji. Pro tento případ číslo mého příspěvkového účtu v rámci ČR je 375486596/2010, ze zahraničí ve formátu IBAN je CZ22 2010 0000 0003 7548 6596.
 

  

🤝 Vaše IP adresa je 18.97.9.174 (18-97-9-174.crawl.commoncrawl.org)